Tetraedrul

    Piramida este figura geometrica ce are ca baza un poligon, iar fetele laterale triunghiuri.

    Elementele geometrice ale unei piramide:

• baza piramidei: ABC;
• fata laterala: VAC, VAB, VBC;
• muchia bazei: AB, AC, BC;
• muchia laterala: VA, VB, VC;
• inaltimea: VO;
• apotema bazei (daca baza este un poligon regulat): OD;
• apotema piramidei (daca piramida este dreapta): VD.

Tipuri:
1. Piramida patrulatera regulata
2. Piramida triunghiulara regulata
3. Piramida hexagonala regulata

Tetraedrul

Definitie: Tetraedrul regulat este piramida triunghiulara (regulata dreapta) cu toate muchiile congruente. Toate cele 4 fete sunt triunghiuri echilaterale congruente. (Fig. 1)

Fig. 1

Elementele tetraedrului: 

• 4 varfuri: A, B, C, D;
• 6 muchii: segmentele [AB], [AC], [AD[, [BC], [BD], [CD];
• 4 fete ( cele 4 triunghiuri echilaterale formate)

Orice fata triunghiulara a tetraedrului poate fi considerata baza.

Formulele tetraedrului: 

Aria bazei	${\displaystyle A_{0}={{\sqrt {3}} \over 4}a^{2}\,}$
Aria totală	${\displaystyle A=4\,A_{0}={\sqrt {3}}a^{2}\,}$
Înălțimea	${\displaystyle {\sqrt {2 \over 3}}\,a\,}$
Volumul	${\displaystyle V={1 \over 3}A_{0}h={{\sqrt {2}} \over 12}a^{3}\,}$
Unghiul dintre o față și muchie	${\displaystyle \arccos \left({1 \over {\sqrt {3}}}\right)=\arctan({\sqrt {2}})\,}$ (aprox. 54.7356°)
Unghiul dintre două fețe	${\displaystyle \arccos \left({1 \over 3}\right)=\arctan(2{\sqrt {2}})\,}$ (aprox. 70.5288°)
Unghiul dintre segmentele care unesc centrul cu două vârfuri	${\displaystyle \arccos \left({-1 \over 3}\right)\,}$ (aprox. 109.4712°)
Unghiul solid sub care este văzută o față din vârful opus	${\displaystyle 3\arccos \left({1 \over 3}\right)-\pi \,}$ (aprox. 0.55129 steradiani)

Exercitii aplicative: 

1. Piramida triunghiulară regulată, dreaptă – tetraedrul regulat:

Aflati:

• Elementele tetraedrului regulat:

AD =

SO =

SD =

• Suma tuturor muchiilor:

• Cel mai scurt drum CM, pe fețele (SAB) și (SBC): 

2. Tetraedrul regulat ABCD are muchia de 6 cm, notam cu M si N mijloacele segmentelor AB si AC.
a) Demonstrati ca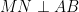 si
b) Calculati lungimea segmentului MN

3.Tetraedrul regulat ABCD are suma muchiilor de 54 cm.Aflați:
a) Aria și volumul tetraedrului
b) Sinusul unghiului format de o față laterală cu planul bazei
c) Dacă DO ^ (ABC) aflați distanța de la punctul O la o față laterală.

4. Fie ABCD este un tetraedru rgulat.
a) Dacă latura tetraedrului este de 6 cm atunci aria laterală este .................. cm2
b) Măsura unghiului format de două muchii ale unui tetraedru este de ........o
c) Sinusul unghiului dintre 2 fețe ale unui tetradru regulat este .....................
d) Dacă aria totală a unui tetraedru regulat este 64 cm2, volumul tetraedrului
este......................cm3 .
e) Dacă volumul unui tetraedru regulat este 16cm3, aria totală a tetraedrului este
de ...................cm2 .
f) Un tetraedru regulat are volumul și aria totală exprimate prin același număr. Aflați
muchia, înălțimea și aria laterală.
g) Dacă segmentul determinat de centrele de greutate a două fețe ale unui tetraedru
este de 18 cm, aflați muchia, înălțimea și aria laterală.
h) Dacă înălțimea unui tetraedru regulat este 3 cm, aflați aria totală si volumul
tetraedrului

5. Fie ABCD un tetraedru regulat, iar M mijlocul lui AD. Dacă aria triunghiului BCM
este de 9 cm2, aflați aria totală a tetraedrului.

6. Aflați aria laterală a unui tetraedru regulat, dacă prin desfășurare se obține un triunghi
echilateral cu aria de 16 cm2.

7. Fie un tetraedru regulat cu muchia de 6 cm. Aflați
a) Aria totală și volumul tetraedrului
b) Distanța de la centrul unei fețe la planul altei fețe
c) Arătați că două muchii opuse sunt perpendiculare
d) Distanța de la mijlocul unei muchii la muchia opusă ei.

8. Fie VABC un tetraedru regulat și M un punct în interiorul lui astfel încât distanțele
de la M la punctele A, B, C, să fie egale cu 12 cm, iar VM = 12 cm. Se cere:
a) Aria totală și volumul tetraedrului ;
b) tangenta unghiului format de muchia laterală cu planul bazei ;
c) distanța de la centrul bazei la o față laterală.

9. Fie SABC un tetraedru regulat și M mijlocul muchiei SC .
a) Arătați că SC (MAB)
b) Arătați că ariile totale ale piramidelor SAMB și MABC sunt egale
c) Aflați raportul volumelor piramidelor SAMB și MABC
d) Determinați poziție unui punctul M pe SC, pentru ca aria triunghiului AMB să fie
minimm?

10. Fie VABC un tetraedru regulat cu înălțimea de 2 cm.
a) Aflați aria totală și volumul tetraedrului
b) Dacă P este mijlocul lui VA, iar înălțimea VO intersectează planul (PBC) în Q,
detrminați determinați valoarea raportului .